Movimiento Armónico Simple

Decimos que una partícula o sistema tiene movimiento armónico simple, cuando vibra bajo acción de fuerza restauradoras que son proporcionales a la distancia respecto a la posición equilibrio. Decimos entonces que dicho cuerpo es un oscilador armónico.

Tipos de vibraciones:

Vibratorio: El cuerpo oscila entorno a una posición de equilibrio siempre en el mismo plano.

Periódico: El movimiento se repite cada cierto tiempo, denominado periodo (T). Es decir, el cuerpo vuelve a tener las mismas magnitudes sinematicas y dinámicas cada T segundos.

Magnitud del movimiento armonico simple

Elongación: Representa la posición de la particula que oscila la funció del tiempo y es la separación del cuerpo de la posición de equilibrio.

Amplitud: Es la elongación máxima.

Frecuencia: Es el numero de oscilasiones o vibraciones que se producen en un segundo.

Periodo: Es el tiempo que tarda en cumplirse una oscilación completa. 

Fase: La fase del movimiento en cuaqluier estante corresponde al angulo que representa el estado de vibración del cuerpo en un instante determinado.

Frecuencia amgular, velocidad angular o pulsación: Representa la velocidad de cambio de la fase del movimiento se trata de periodos comprendidos en 2π segundos.

Pendulo Vibratorio 

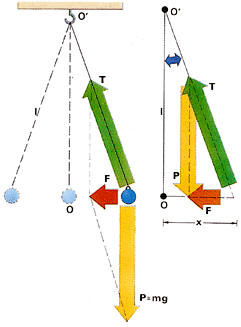
Un péndulo simple está formado, en esencia, por un cuerpo de pequeña extensión, como una bola o un disco, que cuelga de un punto fijo a través de un hilo largo de longitud fija (inextensible) y masa despreciable.

Un estudio dinámico del movimiento del péndulo

El movimiento de un péndulo simple es uno de los muchos movimientos naturales que pueden ser considerados como armónico simples. Para comprobarlo, es preciso efectuar un análisis dinámico del mismo. Las fuerzas que actúan sobre el cuerpo, supuesto aislado, son el peso P y la tensión T del hilo. La suma de ambas, efectuada mediante la composición del triángulo de fuerzas, dará lugar a la fuerza neta o resultante F.

Si el hilo es suficientemente largo, la trayectoria curva de la bola al oscilar de un lado para otro puede considerarse como aproximadamente rectilíneo. Admitiendo tal simplificación, resulta que el triángulo formado por las fuerzas P, T y F es semejante al que forma la línea vertical por el punto de suspensión, la línea horizontal que paralela al techo pasa por el cuerpo, y la línea del hilo. Por tanto, de acuerdo con el teorema de Tales, de semejanza entre triángulos, se tiene:

siendo x la elongación y l la longitud del hilo.

Dado que P = mg, se tiene para la fuerza neta responsable del movimiento:

De acuerdo con la segunda ley de Newton, producirá una aceleración a = F/m, es decir:

(7.18)

en donde el signo - se incluye para recordar que, también en este caso, la fuerza y el desplazamiento tienen signos opuestos.La expresión de la aceleración es del tipo:

a = - cte x

Se trata, por tanto, de la aceleración de un movimiento armónico simple. Identificando en este caso las ecuaciones (7.1) y (7.18) resulta:

(7.19)

es decir:

Las fórmulas de la elongación y de la velocidad del M.A.S. son también aplicables al estudio de un péndulo simple, siempre que los ángulos de desviación (con respecto de la vertical) sean pequeños. Para ello basta

APLICACIÓN DEL MOVIMIENTO ARMONICO SIMPLE:

- Péndulo que se mueve en un reloj.

- Cepillo de dientes eléctrico.

- Las figuras de los gatos chinos de la suerte (que mueve su mano hacia a delante y atrás)

- Campana de una iglesia al sonar.

- Movimiento de una mecedora.

- El aleteo de los colibrís o abejas.